1.4 - Key Stretching

Learning Objectives
1.4 - Explain the importance of using appropriate cryptographic solutions.
- Key stretching
What is Key Stretching?
As time goes on our computer processors become more powerful, allowing them to perform more efficient brute-force attacks against our existing cryptographic security features. While it is possible for more advanced cryptographic functions to be developed to combat this, there is another method to protect our keys using our existing technology.
Key stretching is a cryptographic technique designed to enhance the security of weak keys or passwords by making them computationally expensive to crack. This method involves processing the original input (e.g. a password) through a series of repeated cryptographic operations, typically using hashing functions. The goal is to increase the amount of time and effort required for an attacker to perform brute-force attacks, thereby strengthening the overall security without changing the fundamental way keys are generated or managed.
Think of it like putting your most valuable item into a safe... and then putting that safe into another safe... and so on until you're convinced that the effort required to break through each safe is enough to make any forceful attempt by an attacker completely infeasible.
How Does Key Stretching Work?
In a previous post, we covered the basic concepts of Hashing & Salting. Key stretching essentially repeats this process multiple times on the same piece of data(a "key").
A basic version of this process can be visualised using the diagram below:
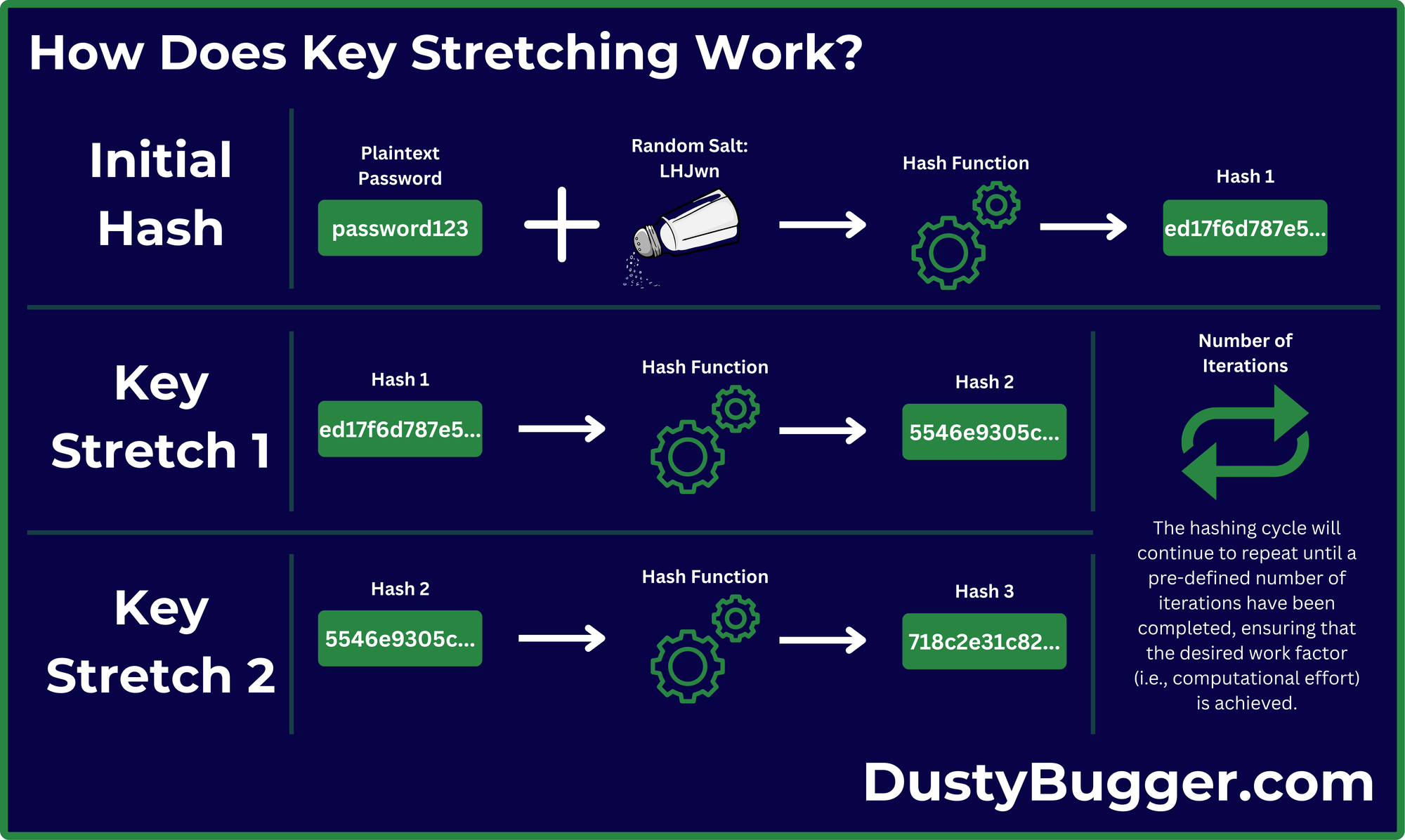
As you can see, we begin with combining a plaintext password and a random Salt before sending it through a hash function (I used SHA256 for this example). Once we have generated our initial hash, we then repeat the process by sending it back through the same hash function as many times as we want until we are confident that our key is secure.
Each iteration slightly increases the processing time. For regular users, this delay is barely noticeable. But for an attacker trying billions of guesses? It becomes painfully slow.
The way we determine how many times to repeat the hashing process is by setting a pre-defined Work Factor:
What is a Work Factor?
A work factor (also called a cost factor) is a configurable setting that determines how computationally expensive the key stretching process will be. In other words, it defines the amount of time and processing power required to generate the final key.
The higher the work factor, the longer it takes to compute each key - which is great for security because it significantly slows down brute-force attacks, making each password guess more costly for an attacker.
For example, without any protection, a single SHA-256 hash might take just 0.001 milliseconds(1 microsecond) to compute. Thus allowing an attacker to attempt 1 million guesses per second. However, if the password is salted and stretched, the attacker must:
- Try every possible password.
- Try every possible salt value with each one of those passwords.
- Repeatedly hash every possible combination of passwords and salts thousands or even millions of times.
This drastically increases the time and computing power needed, making brute-force attacks far less practical.
Why not add a Salt to each iteration?
The primary purpose of a salt is to ensure that users with the same password end up with different hashes. Thus breaking patterns and preventing attackers from using precomputed hash databases (like rainbow tables).
Because of the avalanche effect and the deterministic nature of hashing, applying the salt just once is enough to ensure a unique output, even across millions of hash iterations.
While it’s technically possible to add a salt during each hash iteration, it provides little to no added benefit in terms of real-world security. In fact, doing so would make the process unnecessarily complex.
If you added a different salt in every iteration:
- You’d need to generate and store up to millions of unique salts per password.
- During login, you’d have to recall and apply each salt in the exact same order, just to recreate the final comparison hash.
This approach is inefficient, error-prone, and offers no meaningful gain over simply using a single salt and increasing the number of iterations.
By salting only once at the start and stretching the hash over many rounds, we achieve strong protection with far less overhead - all while storing and managing just one salt per user.
Common Key Stretching Algorithms
There are several well-known key stretching algorithms that achieve similar goals using slightly different implementations:
PBKDF2 (Password-Based Key Derivation Function 2)
PBKDF2 is one of the most commonly used key stretching algorithms. It applies a pseudorandom function, typically a HMAC, to the input and salt repeatedly (as specified by a work factor) and thus resulting in a derived key.
It is widely used in WPA2 Wi-Fi security and many password management tools.
bcrypt
Bcrypt is a key stretching algorithm which is based on the Blowfish cipher. Like PBKDF2 it uses an input, a salt, and multiple iterations to create a stretched output. It is common in web application authentication systems and is specifically designed to hash passwords with the ability to increase the cost factor to counter rising computational power over time.
scrypt
Scrypt is designed to be both computationally and memory-intensive, making it significantly more resistant to large-scale, parallel brute-force attacks using GPUs or ASICs. It achieves this by requiring a substantial amount of memory during the key derivation phase, which dramatically increases the cost of launching hardware-accelerated attacks.
It is primarily used in cryptocurrency processes like Litecoin mining and secure password hashing in some applications.
Final Thoughts
Key stretching is a clever way of squeezing extra security out of something weak - like a short or reused password. While, it doesn’t magically make your password secure, it does significantly slow down attackers and is a critical part of modern cryptographic systems.